Strona główna Finanse Analiza ryzyka finansowego Jakie są miary zmienności?

Jakie są miary zmienności?

Przez

28 czerwca 2025

106

Jakie są miary zmienności?

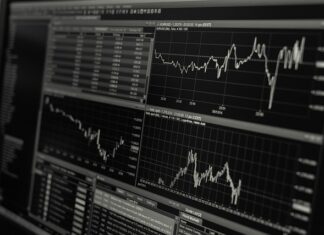
W dzisiejszym artykule przyjrzymy się tematowi miar zmienności. Zmienność jest ważnym pojęciem w wielu dziedzinach, takich jak statystyka, ekonomia, finanse i nauki społeczne. Miary zmienności pozwalają nam zrozumieć, jak dane zmieniają się wokół średniej wartości i jak rozproszone są wokół niej. Są one niezwykle przydatne w analizie danych i podejmowaniu decyzji. W tym artykule omówimy różne miary zmienności, ich zastosowanie i wyzwania z nimi związane.

Wprowadzenie

Zmienność jest miarą rozrzutu danych wokół średniej wartości. Oznacza to, że im większa zmienność, tym bardziej dane są rozproszone wokół średniej. Zmienność jest ważnym pojęciem w statystyce, ponieważ pozwala nam zrozumieć, jak dane się różnią i jakie są ich rozrzuty. Istnieje wiele różnych miar zmienności, które można stosować w zależności od rodzaju danych i celu analizy.

Odchylenie standardowe

Jedną z najpopularniejszych miar zmienności jest odchylenie standardowe. Odchylenie standardowe mierzy, jak bardzo dane różnią się od średniej wartości. Im większe odchylenie standardowe, tym większa zmienność danych. Odchylenie standardowe można obliczyć jako pierwiastek kwadratowy wariancji. Jest to miara, która jest łatwa do zrozumienia i interpretacji. Im mniejsze odchylenie standardowe, tym bardziej dane są skoncentrowane wokół średniej wartości.

Wariancja

Wariancja jest inną popularną miarą zmienności. Jest to średnia kwadratów różnic między wartościami danych a ich średnią. Wariancja mierzy, jak bardzo dane się różnią od średniej wartości. Im większa wariancja, tym większa zmienność danych. Wariancję można obliczyć jako sumę kwadratów różnic między wartościami danych a ich średnią, podzieloną przez liczbę obserwacji. Wariancja jest szczególnie przydatna w analizie danych, ponieważ uwzględnia wszystkie wartości i daje nam ogólny obraz zmienności danych.

Zakres

Zakres jest prostą miarą zmienności, która mierzy różnicę między największą a najmniejszą wartością danych. Im większy zakres, tym większa zmienność danych. Zakres jest łatwy do obliczenia i interpretacji, ale nie uwzględnia wszystkich wartości danych. Może być przydatny jako szybka miara zmienności, ale nie jest tak dokładny jak odchylenie standardowe lub wariancja.

Procentowy zakres

Procentowy zakres jest miarą zmienności, która mierzy różnicę między największą a najmniejszą wartością danych jako procent średniej wartości. Jest to przydatna miara, ponieważ pozwala nam porównać zmienność danych w różnych skalach. Na przykład, jeśli mamy dwie serie danych o różnych średnich wartościach, procentowy zakres pozwoli nam porównać ich zmienność w sposób względny. Im większy procentowy zakres, tym większa zmienność danych w stosunku do ich średniej wartości.

Współczynnik zmienności

Współczynnik zmienności jest miarą względnej zmienności danych. Oblicza się go jako odchylenie standardowe podzielone przez średnią wartość, a następnie mnoży przez 100, aby otrzymać wynik w procentach. Współczynnik zmienności jest przydatny, gdy chcemy porównać zmienność danych o różnych średnich wartościach. Im większy współczynnik zmienności, tym większa względna zmienność danych.

Interkwartylowy zakres

Interkwartylowy zakres jest miarą zmienności, która mierzy różnicę między pierwszym a trzecim kwartylem danych. Kwartyle to wartości, które dzielą dane na cztery równe części. Pierwszy kwartyl to wartość, poniżej której znajduje się 25% danych, a trzeci kwartyl to wartość, poniżej której znajduje się 75% danych. Interkwartylowy zakres jest przydatny, gdy chcemy mierzyć zmienność danych, pomijając skrajne wartości. Im większy interkwartylowy zakres, tym większa zmienność danych wewnątrz środkowej części rozkładu.

Skosność

Skosność jest miarą asymetrii rozkładu danych. Mierzy, czy dane są skoncentrowane wokół średniej wartości, czy też mają tendencję do skupiania się w jednym z końców rozkładu. Skosność może być dodatnia, jeśli dane są skoncentrowane wokół lewego końca rozkładu, lub ujemna, jeśli dane są skoncentrowane wokół prawego końca rozkładu. Skosność jest przydatna, gdy chcemy zrozumieć, jak dane są rozłożone wokół średniej wartości.